Plante și Planete

Formă sau Conținut?

Întrebarea e cunoscută. Răspunsul de asemenea. Este preferat conținutul de calitate, desigur, chiar dacă învelișul, adică forma în care se înveșmântează, nu e pe măsură. Un înveliș atrăgător care ascunde un conținut de proastă calitate sau nici un conținut dezamăgește. Ideal ar fi ca forma să fie pe măsura conținutului și reciproc. Cu alte cuvinte ar trebui să existe un raport intim, organic, între formă și conținut. Ar trebui ca forma să nu poată decât să corespundă conținutului pentru că el, conținutul, ar trebui să dea naștere formei în care se înveșmântează. Natura reușește asta. Pentru Ea e firesc ca forma să corespundă naturii lăuntrice a conținutului creat. Creează cu o eleganță artistică dar ingineresc-pragmatică în același timp. Și asta pentru că formele prin care se exprimă și se manifestă aparțin conținutului și nu-i sunt adăugate din afară în mod aleator. Ceea ce se exprimă și se manifestă devenind astfel obiectul observației, rămâne însă misterios pentru că nu aparține lumii simțurilor fizice. Așa că ceea ce s-a numit aici conținut este el însuși o formă. Și atunci cum poate fi cunoscut adevăratul conținut?

Bobocii diverselor plante au forme geometrice ce aparțin unei familii de suprafețe distincte. Forma arhetip cu care ne întâmpină la prima vedere este doar prima formă. De câte ori se desfac arătându-și „conținutul” nu fac decât să scoată la iveală cea de-a doua formă care revelează și un anumit număr (de exemplu numărul de frunze sau petale). Fie că desfășoară evantaiul frunzelor, petalelor sau prefigurează viitorul fruct, în dinamica lor bobocii nu fac decât să arate noi și noi forme. Pentru că frunza sau fructul sunt tot forme. Nu numai coaja mărului indică o minunată suprafață-formă ci chiar conținutul zemos este tot o formă. Nu e vorba doar de forme geometrice. Așa că până și gustul fructului sau parfumul lui sunt tot forme, chiar în sensul geometric.

Până la urmă totul se reduce la formă…și număr. Natura, de la Atom și până la Om, este îmbibată de Formă și Număr. Nu e locul aici pentru o demonstrație detaliată a acestei Teoreme, însă sunt recomandate cărțile lui Matila Ghyka mai ales cea în care se vorbește despre geometria artei și a vieții după cum, pentru o aprofundare a unora din capitolele ei, sunt recomandate lucrările de filotaxie ca ramură de sine stătătoare a botanicii precum și lucrările de referință ale geometriei sacre. Sunt de recomandat studiile asupra structurii moleculare geometrice a apei, și nu în ultimul rând, o zăbovire în fața cunoscutului tabel al lui Mendeleev și o cunoaștere, chiar superficială, a formelor și numerelor care guvernează atomul conform celui mai recent model al lui.

În lipsa unei argumentări detaliate acest articol va încerca totuși să jaloneze una din căile unei cercetări științifice recente care, așa cum se va vedea, se pare că reușește să ridice un alt văl al misteriosului conținut. Exprimarea e aleasă cu grijă pentru a nu sugera sau trezi aroganța de a crede că el se va revela vreodată în întregime.

De-a lungul întregului secol trecut, intrigați și inspirați de comunicările făcute deja la începutul secolului 20 de Rudolf Steiner, întemeietorul științei spirituale, cercetători independenți ca Hans Jenny (fizician, întemeietorul Kymaticii), Ehrenfried Pfeiffer (inventatorul metodei detectării cancerului cu ajutorul cristalizării sensibile a clorurii de cupru și pionier al metodelor biodinamice în agricultură), Rudolf Hauschka (chimist, întemeietorul laboratorului Wala), Lawrence Edwards (matematician, descoperitorul unui posibil model al morfologiei plantelor folosind principiile geometriei proiective) și mulți alții, au reușit să confirme parte din aceste comunicări ale științei spirituale. Într-un articol scurt e imposibil să fie rezumate toate aceste cercetări. Ne oprim la ultima. Ca urmare a unor măsurători minuțioase, făcute de-a lungul mai multor decenii, ale formelor dinamice ale bobocilor multor specii de plante, a ouălelor multor specii de păsări, ale formei dinamice a organului inimii umane și nu numai, precum și ale vârtejurilor apei și aerului, L. Edwards ajunge la concluzia că modelul matematic comun acestor forme este cunoscut geometriei proiective sub numele de suprafețe și curbe W. Acestea au fost studiate prima dată de Felix Klein și Sophus Lie, celebrii matematicieni, care le-au dat numele de Weg Kurven. În literatura engleză de specialitate ele sunt cunoscute sub numele de path-curves surfaces. Modelul matematic pe care îl oferă aceste curbe și suprafețe nu e doar acel „best fit”, acea cea mai bună potrivire cu datele experimentale ci, conform cu Edwards și alții care i-au preluat cercetările, pare a fi chiar conținut al Naturii. Într-adevăr se poate dovedi că transformările proiective liniare aplicate în mod repetat elementelor spațiului proiectiv (unui punct de exemplu) au drept invariante tocmai aceste curbe și suprafețe. Cu alte cuvinte locul geometric al punctelor, dreptelor sau planelor, „mișcate” de aceste transformări iterate, generează curbele și suprafețele respective. Asta înseamnă că legile geometriei proiective nu oferă un model doar pentru forma ultimă, finită, a creațiilor enumerate mai sus și studiate de L. Edwards ci un model dinamic al întregii metamorfoze. Pentru a înțelege și mai bine acțiunea acestor transformări este sugerată comparația cu omogenizarea conținutului unei cești de cafea prin mișcări continue și singulare ale linguriței. Teorema lui Brouwer, bine cunoscută în matematică, afirmă că indiferent cum omogenizăm lichidul există o moleculă care nu-și schimbă poziția, adică un punct fix, un punct invariant al transformării spațiului, interior ceștii, care este indusă de mișcarea linguriței. Transformările proiective produc „mișcări” ale spațiului proiectiv în el însuși. Acestea au n+1 puncte fixe într-un spațiu proiectiv cu n dimensiuni. In particular spațiul proiectiv tridimensional are 4 asemenea puncte fixe împreună cu întregul tetraedru asociat lor care reprezintă un sistem de referință (ba chiar de coordonate proiective) pentru curbele W și suprafețele generate de ele care la rândul lor sunt invariante ale acestor transformări.

Conform cercetării lui L. Edwards, spațiul proiectiv pare a fi chiar atelierul spațiu-timp de sculptură al Naturii iar principiile geometriei proiective instrumentele ei de sculptură. Ceea ce face geometria proiectivă aptă pentru o asemenea folosire este, pe de o parte, faptul că elementele de la infinit sunt parte a spațiului proiectiv, iar pe de altă parte, tocmai pentru că le-a adoptat cu drepturi depline, faptul că are o natură duală. Punctul este dual planului, planul este dual punctului iar dreapta este duală ei însăși, în așa fel încât forma este creată de plane care vin din infinit și modelează asemenea unor palme de sculptor, înfășurând-o cu activitatea lor. Această activitate pare a se desfășura la întrepătrunderea a două spatii duale, unul care are un plan la infinit care îl înconjoară din exterior, din toate părțile, și e de neatins iar celălalt care are un punct absolut, interiorizat, care e de asemenea de neatins. Între aceste două, punct absolut și plan absolut, se mișcă „lingurița cosmică” a Naturii. În cazul în care două din cele patru puncte fixe aparțin planului de la infinit al spațiului proiectiv, două din fetele plane ale tetraedrului invariant sunt paralele (adică dreapta lor de intersecție aparține și ea planului de la infinit) și singura muchie vizibilă a acestuia este perpendiculară pe aceste două fete paralele, suprafețele invariante ale transformării proiective raportate la un astfel de tetraedru degenerat pot fi boboci, ouă sau vârtejuri. L. Edwards reușește să identifice doi parametrii care guvernează aceste forme, unul (λ) fiind responsabil de structura globală a suprafeței iar celălalt (ε) de felul în care curbele W spiralează în jurul acestei suprafețe, țesând-o. Trecând prin anumite valori critice λ metamorfozează formele aparent închise (boboci sau ouă) în forme deschise (vârtejuri sau vortexuri) care descriu cu o incredibilă acuratețe vârtejurile produse în mod natural în apă sau cele produse în aer (tornade). Mai mult el constată că λ (și deci forma bobocului de plantă) este extrem de sensibil(ă) la pozițiile relative ale diverselor planete din sistemul nostru solar în raport cu poziția Lunii față de Pământ. Mai exact minimele și maximele graficului variației acestui parametru în timp sunt atinse exact în momentul opozițiilor respectiv conjuncțiilor adică atunci când Terra se „aliniază” cu Luna și planeta, cu Terra între Lună și planetă respectiv cu Luna între Terra și planetă. S-au confirmat în acest fel afinitățile dintre diferitele specii de plante și diferitele planete pe care le indica Steiner acum un secol. Nu a făcut-o numai el. Mulți alții au vorbit, pe baza experimentelor, de exemplu despre dependența calității lemnului de momentul tăierii în raport cu pozițiile Lunii față de planete și cele 12 constelații zodiacale. Hauschka și Ehrenfried au făcut cercetări similare ale acestor corelații microcosmos-macrocosmos. Articolul de față nu poate intra în toate detaliile și nu poate discuta toate implicațiile unei asemenea descoperiri, deci nu pretinde că este exhaustiv. Cititorul nu ar trebui să se grăbească să-și formeze o opinie doar pe baza acestui articol. El e menit doar ca semn rutier pe drumurile lecturii, studiului și experimentării. Mai jos se găsesc câteva imagini care au fost lăsate la urmă în mod intenționat precum și rezultatul unei cercetări independente asupra unui nou tip de stup, cercetare care, deși vine din cu totul altă direcție, răspunde întrebării introductive și al cărei rezultat se înrudește cu cele descrise mai sus și înfățișate in cele ce urmează.

 

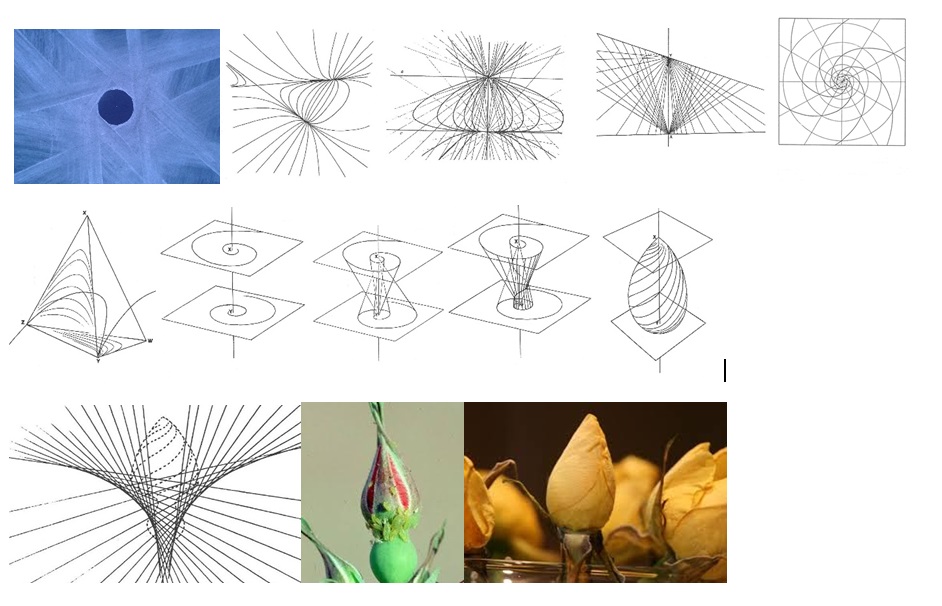
De la stânga la dreapta și de sus în jos:
1. O schiță a autorului articolului înfățișând varianta 2D a interacțiunii dintre infinitul exterior și cel interior, în acest caz dreapta de la infinit a planului și punctul de la infinit al planului dual.
2. Transformarea liniară proiectivă a planului proiectiv, triunghiul fundamental precum și curbele W, invariante ale acestei transformări iterate.
3. Cazul special în care unul dintre vârfurile acestui triunghi este punct la infinit.
4. O situație intermediară care aduce aminte de forma inimii. De fapt se pare că în cazul inimii se suprapun două astfel de forme.
5. Cazul special în care două vârfuri ale triunghiului fundamental sunt puncte la infinit. Se obține astfel spirala logaritmică.
6. Tetraedrul fundamental al transformării proiective a spațiului proiectiv împreună cu curbele W invariante. Se mai numesc și cubice.
7. ( 8,9 și 10) Cele două spirale logaritmice induse pe cele două fete paralele ale tetraedrului degenerat împreună cu produsul finit al suprafeței spiralate a bobocului.
11. Bobocul de trandafir înfășurat de activitatea spațiului dual.
12 și 13. Nu sunt necesare comentariile.
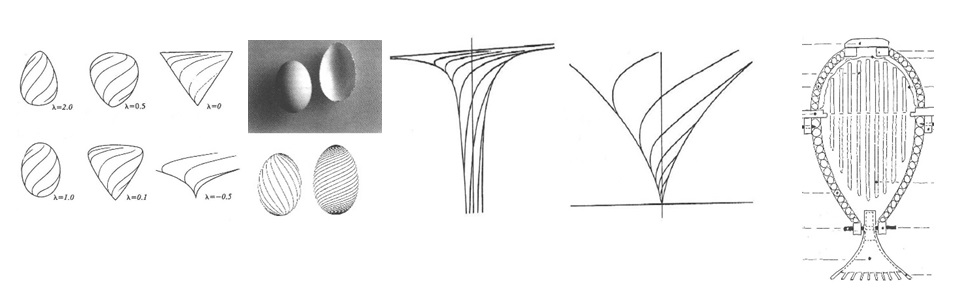
14. Diverse forme corespunzătoare diverselor valori ale lui λ.
15. Ou de rață în realitate dar produs și de o transformare cu un anume λ și un anume ε.
16 și 17. Vârtej de apă și de aer.
18. Un nou tip de stup descris pe scurt în cele ce urmează.

Cu excepția imaginilor 1, 12,13 și 18 restul au fost preluate din cartea „The Vortex of Life” a lui Lawrence Edwards, cu permisiunea editurii. Figura 18 aparține unei cărți al cărui conținut este descris mai jos.

Este interesant și ,după părerea autorului acestui articol, deloc întâmplător că absolut independent și venind dintr-o cu totul altă direcție de cercetare, Günther Mancke, arhitect și apicultor german, inventează un tip de stup care îmbină tradiția coșnițelor cu cea a stupului sistematizat care a fost introdus din motive pragmatice în secolul trecut. Autorul acestui articol a tradus cartea în care cercetătorul german, după două decenii de studii asupra albinelor și preferințelor lor înnăscute, prezintă în detaliu acest nou tip de stup care este conform cu natura lăuntrică a ființei familiei de albine. Exprimarea „natura lăuntrică” este în contextul acestui articol sinonimă cu exprimarea „conținutul lăuntric”. Figura 18 descrie secțiunea longitudinală a acestui înveliș de forma unui ou răsturnat. Forma nu e doar rezultatul unei concepții artistice ci și al unui studiu matematic-ingineresc a ceea ce fac albinele însele. Lanțurile vii formate din albine care încep a secreta ceara și structura fagurele, adică corpul coloniei de albine, se supun legii gravitației luând forma unei curbe cunoscute fizicii și matematicii, numită curbă catenară. Partea inferioară a acestui profil respectă cu exactitate forma unei anumite curbe catenare. Partea superioară este semisferică respectând forma naturală a ghemului sau roiului de albine atunci când iernează sau când, roind, se deplasează unitar prin aer. Detalii despre principiile care au dus la această formă precum și dimensiunile și schițele de lucru se află în această carte a lui Günther Mancke, numită, în traducerea în limba română, Stupul Soarelui.

Ar mai fi multe de dezvăluit. Lăsăm cititorului bucuria de a face conexiunile ce aici au fost doar sugerate și de a porni el însuși pe acest drum. Natura este îmbibată de înțelepciune. Descoperirea ei duce la reverență în fața Naturii și a forțelor inteligente ce se manifestă prin ea. Duce la recunoștință și responsabilitate. Iar în cazul albinelor, și nu numai, responsabilitatea trebuie să ia forme concrete până nu e prea târziu. Inteligența Omului trebuie să fie dublată de capacitatea lui de a avea compasiune adică de iubire pentru tot și toate. Altfel poate deveni distrugătoare și auto-distrugătoare.

Un articol de Florin Secoşan

Cunoaşte Lumea --> Prima pagină